

Behold, a Puzzle
Solution
Filling in the names
The start of the puzzle gives us some text descriptions that reference kinds of quadrilaterals that are typically taught in school, and corresponding enumerations to confirm this. So we start by filling in the blanks at the start with the names of the quadrilaterals they would normally describe. (We could use either TRAPEZOID or TRAPEZIUM for the last blank; it doesn't matter.)
R H O M B U S | All equal sides | ||||||||||||||||||||||||||
R E C T A N G L E | All right angles | ||||||||||||||||||||||||||
S Q U A R E | All right angles, all sides are equal | ||||||||||||||||||||||||||
P A R A L L E L O G R A M | Opposite sides are equal | ||||||||||||||||||||||||||
K I T E | Two pairs of consecutive equal sides | ||||||||||||||||||||||||||
T R A P E Z O I D | Two pairs of consecutive supplementary angles |
The highlighted letters spell out the cluephrase USE AREA, which we use later.
Behold
The heart of the puzzle consists of an image showing the 24 black segments and curves. Since there were six different quadrilaterals earlier and 6 × 4 = 24, this strongly suggests that we should try to assemble the shapes into six quadrilaterals satisfying the definitions given earlier.
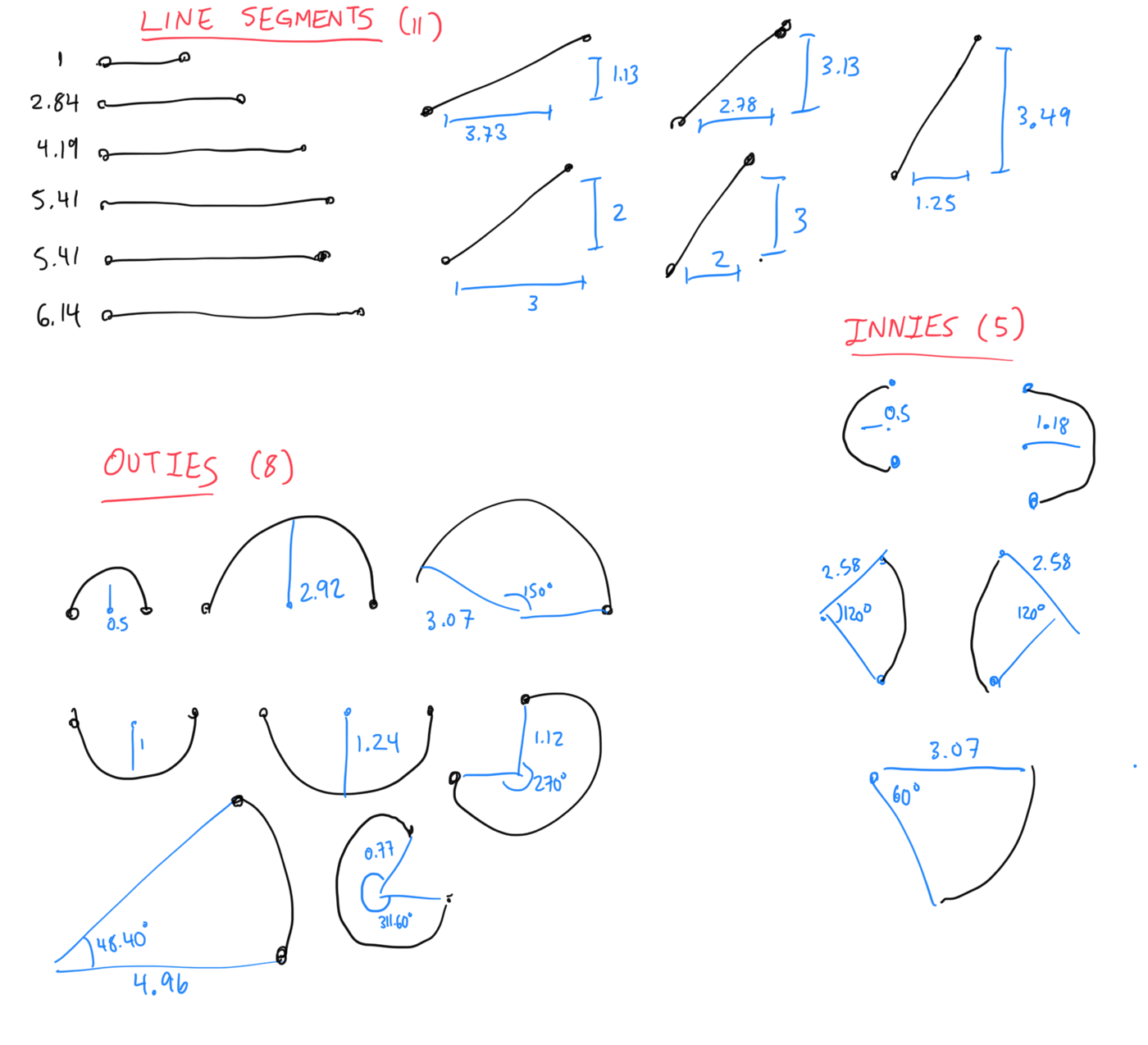
This can be confirmed further when we observe that several of the segments and arcs have equal lengths (up to rounding discrepancies): for example, a 120° circular arc of radius 2.58 has length 2π/3 × 2.58 ≈ 5.403 and thus matches the segments of line 5.41.
The gimmick is that the presence of arcs means that the "definitions" of the quadrilaterals need to be interpreted rather literally. For example, one could normally define a parallelogram as a quadrilateral having opposite sides parallel, but this definition wouldn't make sense. However, having opposite sides of equal length (the definition given in the puzzle) would make sense even if the sides are curved.
This is not the first time this has been done: the title of the puzzle is a reference to the Behold a Square post, an image showing a keyhole-like quadrilateral proposed as a "square". (The name of the meme seems to in turn come from a story where ancient Greek philosopher Diogenes objected to Plato's definition of a man as a "featherless biped". Diogenes allegedly brought a plucked chicken and declared, "Behold, a man!".)
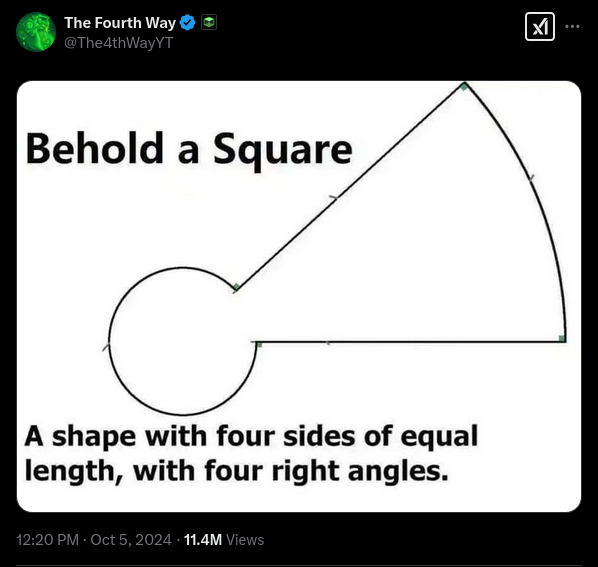
Behold a Square. A shape with four sides of equal length, with four right angles.
(Naturally, the keyhole shape is one of the six shapes present in this puzzle, as a homage to the original post.)
Assembly
Rules
Trying to assemble the pieces, we can infer two important rules:
- The pieces do not need to be rotated. It might have seemed strange initially that some of the segments were given slanted. But piecing together the quadrilaterals, this is for good reason: these are the rotations of the pieces in the assembled figure.
- Some arcs point inwards and others point outwards. This explains the "outies" and "innies" headings.
Strategy
Before assembling the pieces, it's useful to annotate each piece with the following information.
- For each piece, we should compute the length of the segment or arc. Many of the definitions rely on equal lengths, so this can be used to help figure out which pieces go together with which shapes.
- For each piece, we also compute the vector pointing from one endpoint to another. Then in each quadrilateral, the four vectors should add to zero once the direction of the piece is worked out correctly.
These annotations are listed in the Appendix.
The completed shapes
With no apologies whatsoever, we present to you six quadrilaterals (in the order given by the puzzle).
Rhombus (all equal sides)

Rectangle (all right angles)

Square (all right angles, all sides are equal)

Parallelogram (opposite sides are equal)

Kite (two pairs of consecutive equal sides)

Trapzeoid (two pairs of consecutive supplementary angles)

Area extraction
For each cursed shape, as suggested by the earlier cluephrase, we compute the area. This is a straightforward (albeit sometimes annoying) math problem described by one testsolver as "the most MathCounts thing ever".
Each shape has been chosen so that (up to small rounding errors) the area of the shape is an integer from 1 to 26. The areas are given below (in the order that the names were presented).
| Shape | Area | Letter |
|---|---|---|
| Rhombus | 16 | P |
| Rectangle | 15 | O |
| Square | 12 | L |
| Parallelogram | 9 | I |
| Kite | 3 | C |
| Trapezoid | 25 | Y |
Reading off the letters gives the answer POLICY.
Appendix: Math annotations for the assembly step
Here are all 24 pieces with the two annotations we just mentioned, which one can do for each piece independently before trying to assemble them. (We have dx and dy both positive here for line segments; for the arcs, we travel counterclockwise.)
| Kind | dx | dy | Len. | Rad. | Arc angle | Order | Shape |
|---|---|---|---|---|---|---|---|
| Line segments | 1.00 | 0.00 | 1.00 | 1 | RECTANGLE | ||
| Line segments | 2.84 | 0.00 | 2.84 | 2 | RECTANGLE | ||
| Line segments | 4.19 | 0.00 | 4.19 | 3 | SQUARE | ||
| Line segments | 5.41 | 0.00 | 5.41 | 4 | RHOMBUS | ||
| Line segments | 5.41 | 0.00 | 5.41 | 5 | RHOMBUS | ||
| Line segments | 6.14 | 0.00 | 6.14 | 6 | TRAPEZOID | ||
| Line segments | 3.73 | 1.13 | 3.90 | 7 | PARALLELOGRAM | ||
| Line segments | 2.78 | 3.13 | 4.19 | 8 | SQUARE | ||
| Line segments | 1.25 | 3.49 | 3.71 | 9 | PARALLELOGRAM | ||
| Line segments | 3.00 | 2.00 | 3.61 | 10 | KITE | ||
| Line segments | 2.00 | 3.00 | 3.61 | 11 | KITE | ||
| Outies | -1.00 | 0.00 | 1.57 | 0.50 | 180° | 12 | KITE |
| Outies | -5.84 | 0.00 | 9.17 | 2.92 | 180° | 13 | RECTANGLE |
| Outies | -5.73 | 1.54 | 8.04 | 3.07 | 150° | 14 | TRAPEZOID |
| Outies | 2.00 | 0.00 | 3.14 | 1.00 | 180° | 15 | RECTANGLE |
| Outies | 2.48 | 0.00 | 3.90 | 1.24 | 180° | 16 | PARALLELOGRAM |
| Outies | 1.12 | 1.12 | 5.28 | 1.12 | 270° | 17 | TRAPEZOID |
| Outies | -1.67 | 3.71 | 4.19 | 4.96 | 48.40° | 18 | SQUARE |
| Outies | 0.26 | -0.58 | 4.19 | 0.77 | 311.60° | 19 | SQUARE |
| Innies | 0.00 | -1.00 | 1.57 | 0.50 | 180° | 20 | KITE |
| Innies | 0.00 | 2.36 | 3.71 | 1.18 | 180° | 21 | PARALLELOGRAM |
| Innies | 0.00 | 4.47 | 5.40 | 2.58 | 120° | 22 | RHOMBUS |
| Innies | 0.00 | -4.47 | 5.40 | 2.58 | 120° | 23 | RHOMBUS |
| Innies | 1.54 | 2.66 | 3.21 | 3.07 | 60° | 24 | TRAPEZOID |
And here's the same table resorted by the "Shape" column, and minus signs applied so that the dx and dy values in each shape add to 0.
| Kind | dx | dy | Len. | Rad. | Arc angle | Order | Shape |
|---|---|---|---|---|---|---|---|
| Line segments | 5.41 | 0.00 | 5.41 | 4 | RHOMBUS | ||
| Line segments | -5.41 | 0.00 | 5.41 | 5 | RHOMBUS | ||
| Innies | 0.00 | 4.47 | 5.40 | 2.58 | 120° | 22 | RHOMBUS |
| Innies | 0.00 | -4.47 | 5.40 | 2.58 | 120° | 23 | RHOMBUS |
| Line segments | 1.00 | 0.00 | 1.00 | 1 | RECTANGLE | ||
| Line segments | 2.84 | 0.00 | 2.84 | 2 | RECTANGLE | ||
| Outies | -5.84 | 0.00 | 9.17 | 2.92 | 180° | 13 | RECTANGLE |
| Outies | 2.00 | 0.00 | 3.14 | 1.00 | 180° | 15 | RECTANGLE |
| Line segments | 4.19 | 0.00 | 4.19 | 3 | SQUARE | ||
| Line segments | -2.78 | -3.13 | 4.19 | 8 | SQUARE | ||
| Outies | -1.67 | 3.71 | 4.19 | 4.96 | 48.40° | 18 | SQUARE |
| Outies | 0.26 | -0.58 | 4.19 | 0.77 | 311.60° | 19 | SQUARE |
| Line segments | 3.73 | 1.13 | 3.90 | 7 | PARALLELOGRAM | ||
| Line segments | -1.25 | -3.49 | 3.71 | 9 | PARALLELOGRAM | ||
| Outies | -2.48 | 0.00 | 3.90 | 1.24 | 180° | 16 | PARALLELOGRAM |
| Innies | 0.00 | 2.36 | 3.71 | 1.18 | 180° | 21 | PARALLELOGRAM |
| Line segments | 3.00 | 2.00 | 3.61 | 10 | KITE | ||
| Line segments | -2.00 | -3.00 | 3.61 | 11 | KITE | ||
| Outies | -1.00 | 0.00 | 1.57 | 0.50 | 180° | 12 | KITE |
| Innies | 0.00 | 1.00 | 1.57 | 0.50 | 180° | 20 | KITE |
| Line segments | 6.14 | 0.00 | 6.14 | 6 | TRAPEZOID | ||
| Outies | -5.73 | 1.54 | 8.04 | 3.07 | 150° | 14 | TRAPEZOID |
| Outies | 1.12 | 1.12 | 5.28 | 1.12 | 270° | 17 | TRAPEZOID |
| Innies | -1.54 | -2.66 | 3.21 | 3.07 | 60° | 24 | TRAPEZOID |